파이썬 SW문제해결 기본 - LIST 1
05 Sort(정렬)-카운팅 정렬

이번 글은 지난 글(버블 정렬)과 이어지는 글이다. 아래 링크에서 이전 글을 먼저 확인하기를 권장한다.
[SWEA]파이썬 SW문제해결 기본 - LIST 1 : Sort(정렬)-버블 정렬
05. Sort
③ 카운팅 정렬
▣카운팅 정렬
- 항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여, 선형 시간(O(n+k)에 정렬하는 효율적인 알고리즘이다.
- 시간 복잡도 = O(n+k) : n은 리스트의 크기, k는 정수의 최대값
- 정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능하다. 각 항목의 발생 회수를 기록하기 위해, 정수 항목으로 인덱스되는 카운트들의 리스트를 사용하기 때문이다.
- 카운트들을 위한 충분한 공간을 할당하려면 집합 내의 가장 큰 정수를 알아야 한다.
▣ [0, 4, 1, 3, 1, 2, 4, 1]을 카운팅 정렬하는 과정
1. Data에서 각 항목들의 발생 회수를 세고, 정수 항목들로 인덱스 되는 카운트 리스트 COUNTS에 저장한다.
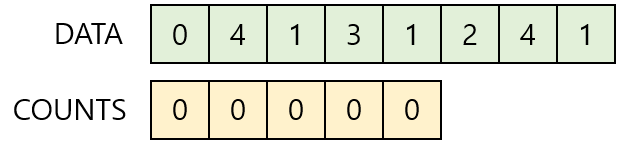
DATA의 최대값이 '4'이므로 COUNTS의 마지막 인덱스는 4(크기 5)가 된다.
2. 정렬된 집합에서 각 항목의 앞에 위치할 항목의 개수를 반영하기 위해 COUNTS의 원소를 조정한다.
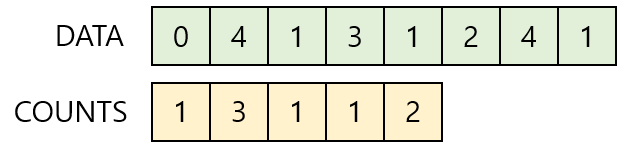
0이 1개이므로 COUNTS[0] = 1
1이 3개이므로 COUNTS[1] = 3
2이 1개이므로 COUNTS[1] = 1
3이 1개이므로 COUNTS[1] = 1
4이 2개이므로 COUNTS[1] = 2
위 값을 누적시키면 다음과 같이 된다.

COUNTS = [1, 1+3, 1+3+1, 1+3+1+1, 1+3+1+1+2]
3. DATA의 마지막 항목 부터 원소를 정렬한다.
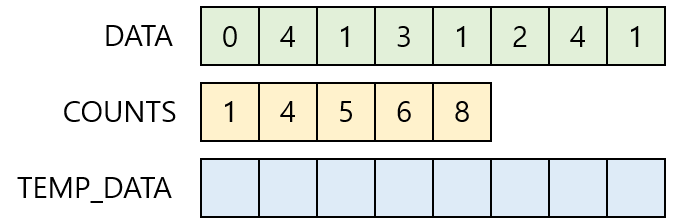
1) 현재 DATA의 마지막 원소는 '1'이다. (Index=7)
2) COUNTS[1]을 1 감소시킨다. (COUNTS[1]=4 --> COUNTS[1]=3)
3) COUNTS[1]이 '3'이므로 TEMP_DATA[3]에 '1'을 삽입한다.
위 과정을 진행하면 다음과 같이 된다.
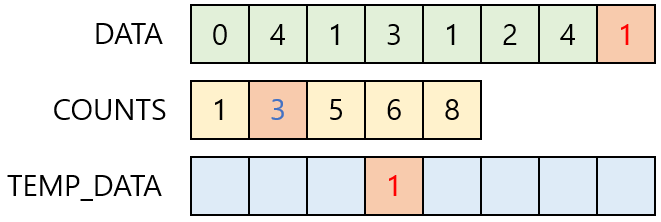
앞선 과정을 반복적으로 진행하면 다음과 같이 된다.
Index=6

Index=5
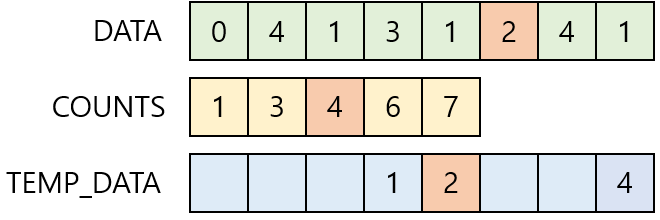
Index = 4
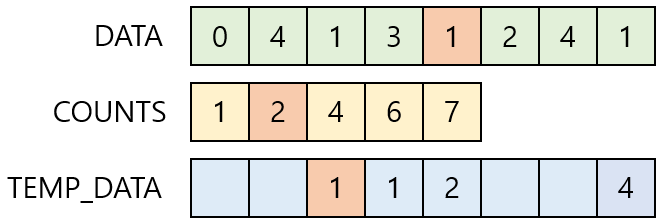
Index = 3
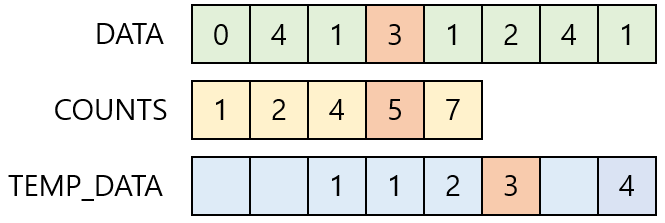
Index = 2
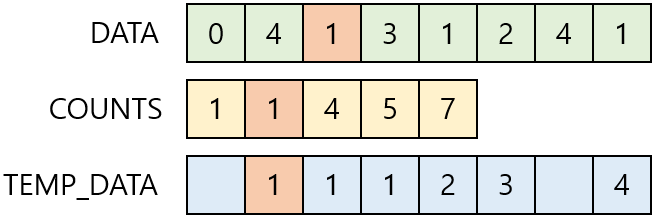
Index = 1
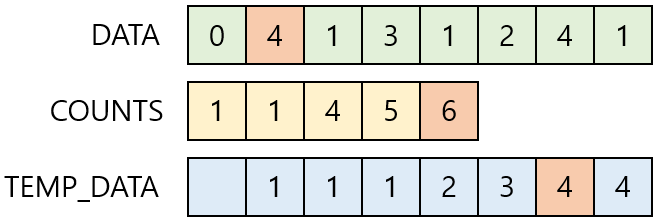
Index = 0
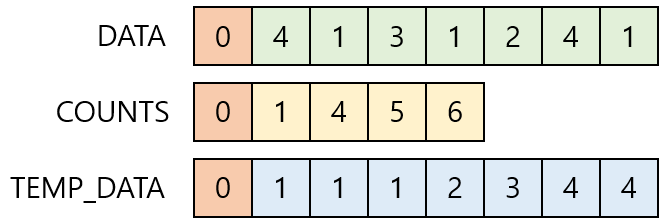
마지막으로 DATA를 TEMP_DATA로 업데이트하면 정렬 작업이 종료된다.
▣ 카운팅 정렬의 Python 구현
def countSort(DATA):
TEMP_DATA = [0 for i in range(len(DATA))]
#본문에서 MAX(DATA)로 최대값을 지정하는 것과 달리 COUNT의 최대 크기를 256으로 제한했다.
COUNT = [0 for i in range(256)]
ans = ["" for _ in DATA]
for i in DATA:
COUNT[ord(i)] += 1
for i in range(256):
COUNT[i] += COUNT[i-1]
for i in range(len(DATA)):
TEMP_DATA[COUNT[ord(DATA[i])]-1] = DATA[i]
COUNT[ord(DATA[i])] -= 1
for i in range(len(DATA)):
ans[i] = TEMP_DATA[i]
return ans▣ 정렬 알고리즘 및 특징
| 알고리즘 | 평균 수행시간 | 최악 수행시간 | 알고리즘 기법 | 비고 |
| 버블 정렬 | O(n^2) | O(n^2) | 비교와 교환 | 코딩이 가장 손쉬움 |
| 카운팅 정렬 | O(n+k) | O(n+k) | 비교환 방식 | n이 비교적 작을 때만 가능 |
| 선택 정렬 | O(n^2) | O(n^2) | 비교와 교환 | 교환의 회수가 버블, 삽입정렬보다 적음 |
| 퀵 정렬 | O(n log n) | O(n^2) | 분할 정복 | 평균 수행시간이 가장 빠름 |
| 삽입 정렬 | O(n^2) | O(n^2) | 비교와 교환 | n의 개수가 작을 때 효과적 |
| 병합 정렬 | O(n log n) | O(n log n) | 분할 정복 | 연결 리스트의 경우 가장 효율적인 방식 |
'SWEA() > Intermediate_Learn' 카테고리의 다른 글
| [SWEA]4831. 파이썬 SW문제해결 기본 - LIST 1 : 전기버스 (0) | 2021.10.18 |
|---|---|
| [SWEA]4828. 파이썬 SW문제해결 기본 - LIST 1 : min max (0) | 2021.10.17 |
| [SWEA]파이썬 SW문제해결 기본 - LIST 1 : Sort(정렬)-버블 정렬 (0) | 2021.10.15 |
| [SWEA]파이썬 SW문제해결 기본 - LIST 1 : Greedy Algorithm (0) | 2021.10.13 |
| [SWEA]파이썬 SW문제해결 기본 - LIST 1 : Exhaustive Search(완전 탐색) (0) | 2021.10.12 |